소수를 판별하는 알고리즘과, N 이하의 소수를 모두 구하는 알고리즘에 대하여 알아보자
- 방법 1 - N 보다 작은 자연수들로 모두 나눠보자
가장 기본적인 방법 중 하나.
임의의 수 N이 1과 N을 제외한 다른 수를 약수로 가지고 있다면 그 수(N)은 소수가 아니고, 다른 약수가 없다면 그 수는 소수일 것이다.
알고리즘
public class Prime_1 {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
prime(in.nextInt());
}
public static void prime(int prime) {
// 0과 1은 소수가 아니다
if(number < 2) {
System.out.println("소수가 아니다");
return;
}
// 2는 소수다
if (number == 2) {
System.out.println("소수");
return;
}
for (int i = 2; i < number; i++) {
// 소수가 아닐 때
if (number % i == 0) {
System.out.println("소수가 아니다");
return;
}
}
// 반복문에서 약수를 가지고 있지 않으면 그 수는 소수.
System.out.println("소수");
return;
}
}
2이상 N 미만의 수 중에 나누어 떨어지는 수가 있다면 소수가 아닌 것을 이용한 소수 판별법
또한, 위 알고리즘의 시간 복잡도는 N 이하의 수까지 모든 수를 검사하므로 O(N)이다.
N 이하의 모든 소수를 구하는 알고리즘
위의 알고리즘을 응용하여 N 이하의 소수를 모두 구하는 알고리즘은 다음과 같을 것
public class Prime_1 {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int N = in.nextInt();
// 0 ~ N 까지 수 중 소수를 구하는 반복문
for(int i = 0; i <= N; i++) {
prime(i);
}
}
//소수 생성 메소드
public static void prime(int number) {
// 0과 1은 소수가 아니다
if(number < 2) {
return;
}
// 2는 소수다
if (number == 2) {
System.out.println(number);
return;
}
for (int i = 2; i < number; i++) {
// 소수가 아닐 때
if (number % i == 0) {
return;
}
}
// 반복문에서 약수를 가지고 있지 않으면 그 수는 소수.
System.out.println(number);
return;
}
}
이 알고리즘은 소수 판별 알고리즘을 N 번 반복하여 각 수마다 소수를 판별한 뒤 소수만 출력하는 알고리즘
즉, O(N) 알고리즘을 N 번 반복하므로, 위 방법의 N 이하의 소수를 모두 구하는 알고리즘의 시간복잡도는 O(N^2)이다.
- 방법 2 - √N 이하의 자연수들로 모두 나눠보기
방법 1의 방법에서 약간 업그레이드 된 알고리즘
N을 √N 이하의 자연수들만 나누는 방법.
이유는? - 소수를 판별한다는 것은 결국 1과 자기 자신을 제외한 다른 자연수를 약수로 갖고 있으면 안된다는 말이다.
임의의 자연수 N(N > 0) 이 있다고 가정
p X q = N을 만족할 때 우리는 아래와 같은 부등식을 완성할 수 있다.
(1 <= p, q <= N)
그리고 p와 q중 하나는 √N 보다 작거나 같다.
예를 들면, N = 8 일 때,
1 X 8
2 X 4
4 X 2
8 X 1
이렇게 볼 수 있듯, 만약 p가 증가한다면 자연스레 q가 감소하고,
반대로 p가 감소하면 q가 증가한다.
그리고 p와 q는 N의 약수이기 때문에 결국 N을 임의의 수로 나누게 되면, 임의의 수가 √N 보다 작다면 결국 나머지는 √N보다 클 수 밖에 없다.
결국 p와 q 중 하나는 반드시 √N 보다 작거나 같다.
즉, √N 이하의 자연수 중에 나누어 떨어지는 수가 있다면 이는 1과 N을 제외한 다른 자연수가 N의 약수라는 의미이므로 소수가 아니게 되는 것이다.
√N 을 사용한 소수 판별 알고리즘
public class Prime_2 {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
prime(in.nextInt());
}
public static void prime(int number) {
// 0과 1은 소수가 아니다
if(number < 2) {
System.out.println("소수가 아니다");
return;
}
// 2는 소수다
if (number == 2) {
System.out.println("소수");
return;
}
// 제곱근 함수 : Math.sqrt()
for (int i = 2; i < Math.sqrt(number); i++) {
// 소수가 아닐 때
if (number % i == 0) {
System.out.println("소수가 아니다");
return;
}
}
// 반복문에서 약수를 가지고 있지 않으면 그 수는 소수.
System.out.println("소수");
return;
}
}
2 이상 √N 이하의 수 중에 나누어 떨어지는 수가 존재한다면 소수가 아님을 이용한 소수 판별법이다.
또한, 이 알고리즘의 시간복잡도는 √N 이하의 수까지 모든 수를 검사하므로 O(√N)이다.
N 이하의 모든 소수를 구하는 알고리즘
이를 응용한 N 이하의 소수를 구하는 알고리즘
public class Prime_2 {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int N = in.nextInt();
for (int i = 0; i <= N; i++) {
prime(i);
}
}
// 소수 생성 메소드
public static void prime(int number) {
// 0과 1은 소수가 아니다
if(number < 2) {
return;
}
// 2는 소수다
if (number == 2) {
return;
}
// 제곱근 함수 : Math.sqrt()
for (int i = 2; i < Math.sqrt(number); i++) {
// 소수가 아닐 때
if (number % i == 0) {
return;
}
}
// 반복문에서 약수를 가지고 있지 않으면 그 수는 소수.
System.out.println("소수");
return;
}
}
이 알고리즘은 소수 판별 알고리즘을 N 번 반복하여 각 수마다 소수를 판별한 뒤 소수만 출력하도록 한 알고리즘.
즉, O(√N) 알고리즘을 N 번 반복하므로, 위 방법의 N 이하의 소수를 모두 구하는 알고리즘의 시간복잡도는 O(N√N)이다.
- 방법3 : 에라토스테네스의 체 - k = 2부터 √N 이하까지 반복하여 자연수들 중 k를 제외한 k의 배수들을 제외시킨다
방법은 이렇다.
k = 2 이면, 2를 제외한 2의 배수를 모두 지우고,
k = 3 이면, 3을 제외한 3의 배수를 모두 지우고,
(k = 4는 이미 2 일 때, 제외되어 넘어감)
k = 5 이면, 5를 제외한 5의 배수를 모두 지워주면서
k = √N 까지 반복하는 방법이다.
N이하의 모든 소수를 구하는 알고리즘
public class Prime_3 {
public static boolean[] prime; // 소수를 체크할 배열
public static void mian(String[] args) {
Scanner in = new Scanner(System.in);
int N = in.nextInt();
prime(N);
for (int i = 0; i < prime.length; i++) {
if(prime[i] == false) { // 소수(false)일 경우 출력
System.out.println(i);
}
}
}
// N 이하의 소수 생성 메소드
public static void prime(int N) {
prime = new boolean[N + 1]; //배열의 특징을 기억할 것
// 소수가 아닌 index = true
// 소수인 index = false
if (N < 2) {
return;
}
prime[0] = prime[1] = true;
// 제곱근 함수 : Math.sqrt()
for (int i = 2; i <= Math.sqrt(N); i++) {
// 이미 체크된 배열이면 다음 반복문으로 skip
if(prime[i] == true) {
continue;
}
// i의 배수들을 걸러주기 위한 반복문
for (int j = i * i; j < prime.length; j = j + i) {
prime[j] = true;
}
}
}
}
해당 알고리즘은 이중 for 문이라 시간복잡도가 O(N^2)일 것 같지만 그렇지 않다.
이유는? - 1 ~ x 까지의 수가 있는 칸을 체크하는 횟수를 대략적으로 따진다면 아래와 같을 것이다.
(n = 1 부터 시작한다고 가정)
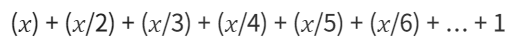
그렇다면 위 식을 간략하게 표현하면

위의 x로 묶인 괄호 안의 수열은 '조화 수' 라고 하는데, 이는 조화 수열에서 부분 합을 말한다고 한다.
그리고 다음과 같이 발산을 한다고 한다.

이 때, 감마는 상수 값이고 O(1/x)는 우리가 생각하는 big O와 같은 표기로 수학에서는 함수 성장률의 상한선이다. 그리고 위의 조화 수는 대략 자연로그의 형태를 따라간다.
즉, N 이하의 소수에 대하여 체에 거르는 시간이 log N 이므로 단순하게 체에 거르는 것만 해도 시간복잡도는 O(N log N)이다. (log는 자연로그 ln으로 본다)
그런데, 여기서 우리는 더 나아가 이미 체크된 배열은 검사하지 않고 다음 반복문으로 넘어간다.
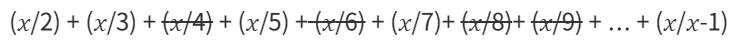
우리는 앞에서 조화 수를 통해 점근적 시간복잡도 O(N log N) 이라는 시간복잡도를 얻었다.
이 의미는 x개의 수에 대해 2일 때 체크하는 개수인 (x/2), 3일 때 체크하는 개수인 (x/3)... 이렇게 체크를 하게 된다.
하지만, 우리가 알고 싶은 것은 이미 중복되는 수들을 검사하지 않는 것!
이 의미는 결국 검사하는 수는 소수로 판정될 때 그의 배수들을 지우는 것이라는 것이다.
즉, 이 말은 구간 내의 소수의 개수를 알아야 한다는 뜻이기도 하다.
근데 소수는 규칙성이 없고, 가우스의 소수 정리에 따르면
x보다 작거나 같은 소수의 밀도에 대해 대락 1 / ln(x) 라는 것이다.
즉, 이를 거꾸로 말하면 x번째 소수는 x log(x)라는 의미가 되는 것이다.
실제로 보면, 앞서 1/x의 합을 구했지만, 중복되는 수가 제외된다면 x는 소수만 된다는 의미고, 이는 소수의 역수 합이다.
(1/2 + 1/3 + 1/5 + 1/7 + ....) 이런 식이다.
그러면 시간복잡도는 O(N log(logN))의 시간복잡도를 가지게 된다.
'ssung_끄적끄적 > JAVA_끄적' 카테고리의 다른 글
| 배열의 오름차순, 내림차순 (0) | 2023.08.18 |
|---|---|
| 특수문자 출력하기 ( 괄호, 백슬래시, 따옴표 등등) (0) | 2023.07.28 |
| substring vs split 문자열 자르기 (0) | 2023.07.21 |
| replace와 replaceAll (0) | 2023.06.21 |